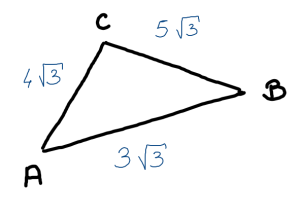
Exercice 9
On considère le triangle ABC dont les cotés mesurent :
\(AB = 3\sqrt{3}\)
\(BC=5\sqrt{3}\)
\(CA=4\sqrt{3}\)
Question
Quelle est la nature de ce triangle ? « Justifier votre réponse »
Indice
Commencer par dessiner un schéma correctement renseigné pour traduire l’énoncé.
Solution
On a : un tringle ABC dont on connaît les longueurs des trois cotés
\(AB = 3\sqrt{3}=\sqrt{9 \times 3}=\sqrt{27}\)
\(BC=5\sqrt{3}=\sqrt{25 \times 3}=\sqrt{75}\)
\(CA=4\sqrt{3}=\sqrt{16 \times 3}=\sqrt{48}\)
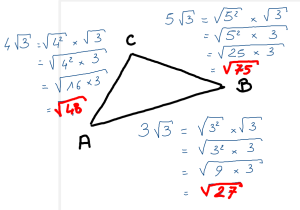
On utilise : la réciproque du théorème de Pythagore :
Si dans un triangle la somme du carré de deux cotés est égale au carré du troisième coté
Alors ce triangle est un triangle rectangle.
On obtient :
\(AB^2=27\)
\(BC^2=75\)
\(CA^2=48\)
on remarque que 27 + 48 = 75 soit \(AB^2+CA^2=BC^2\)
Attention : Conclusion
Le triangle ABC est un triangle rectangle en A
AB et CA sont les deux cotés de l'angle droit
BC est l’hypoténuse