Dérivation - Ex15
La parabole \(\mathscr P\) a pour équation \(y=x^2\).
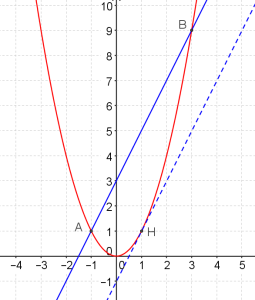
On considère les points \(A\) et \(B\) de \(\mathscr P\) d'abscisses respectives \(-1\) et \(3\).
Question
1) Peut-on trouver une tangente à \(\mathscr P\) qui est parallèle à \((AB)\) ? Si oui, en quel(s) point(s) ?
Solution
Les points sont
\(A(-1 ;f(-1))=\color{blue}(-1 ;1)\)
\(B(3 ;f(3))=\color{blue}(3 ;9)\).
La droite \((AB)\) a pour coefficient directeur : \(\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{9-1}{3-(-1)}\,\color{blue}=2\)
Trouver une tangente parallèle à \((AB)\) revient à trouver \(x\) tel que \(f'(x)=2\).
\(f(x)=x^2\) donc \(f'(x)=2x\).
\(f'(x)=2 \iff 2x=2\iff \color{red}\underline{x=1}\)
Au point d'abscisse \(\color{red}H(1 ;f(1))=(1 ;1)\), la tangente est parallèle à \((AB)\).
On peut en faire une vérification graphique.
Question
2) De manière générale, si \(A\) et \(B\) sont deux points quelconques de \(\mathscr P\), existe-t-il toujours une tangente à \(\mathscr P\) parallèle à \((AB)\) ?
Si oui, comment la construire géométriquement ?
Solution
On considère les points \(A(a ;a^2)\) et \(B(b ;b^2)\) appartenant à la parabole \(\mathscr P\) avec \(a,\,b\in\mathbb R\).
Le coefficient directeur de la droite \((AB)\) est égal à :
\(\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{b^2-a^2}{b-a}=\dfrac{(b-a)(b+a)}{b-a}=\color{blue}a+b\)
On cherche donc \(x\) tel que \(f'(x)=a+b\) :
\(f(x)=x^2\) donc \(f'(x)=2x\)
\(f'(x)=a+b\iff 2x=a+b\iff\color{red}\underline{x=\dfrac{a+b}{2}}\) (c'est la moyenne des valeurs \(a\) et \(b\))
Si les points \(A\) et \(B\) ne sont pas confondus, il existe toujours une tangente à \(\mathscr P\) qui soit parallèle à \((AB)\).
Elle passe par le point \(\color{red}H\left(\dfrac{a+b}{2} ;\dfrac{(a+b)^2}{4}\right)\).
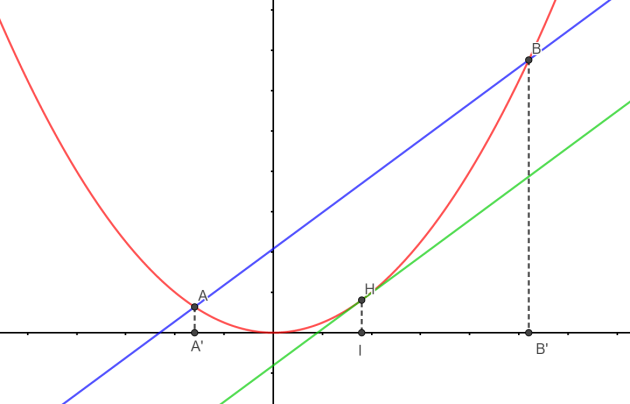
Pour la construire géométriquement, on construit :
sur l'axe des abscisses, le milieu \(I\) du segment \([A'B']\) avec \(A'(a ;0)\) et \(B'(b ;0)\). \(I\) a pour abscisse \(\dfrac{a+b}{2}\),
le point \(H\) de la parabole d'abscisse \(\dfrac{a+b}{2}\) (la même que \(I\)),
la parallèle à \((AB)\) passant par \(H\).
Fichier GeoGebra à télécharger :
