Dérivation - Ex14
Soit \(f\,\colon x\mapsto\dfrac{x^2-3x+6}{x-1}\) et \(\mathscr C\) sa courbe représentative.
Question
1) Préciser l'ensemble de définition de \(f\).
Solution
On doit avoir \(x-1 \neq 0 \iff\underline{x \neq 1}\).
\(\color{red}\underline{D_f=]-\infty ;1[\cup]1 ;+\infty[=\mathbb R \smallsetminus\{1\}}\)
Question
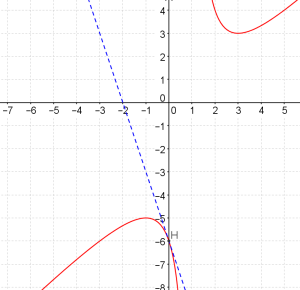
2) Donner les coordonnées du point \(H\) où \(\mathscr C\) coupe l'axe des ordonnées.
Solution
On calcule \(f(0)\).
\(f(0)=\dfrac{0^2-3\times 0+6}{0-1}=\underline{-6}\)
\(\color{red}\underline{H(0 ;-6)}\)
Question
3) Déterminer la tangente \(T\) à la courbe \(\mathscr C\) au point \(H\).
Solution
On détermine la fonction dérivée :
\(f\) est du type \(\dfrac{{\color{blue}u}}{{\color{red}v}}\) avec \(\color{blue}u\) et \(\color{red}v\) dérivable sur \(\mathbb R \smallsetminus \{1\}\) donc \(f\) est dérivable sur \(\mathbb R \smallsetminus \{1\}\).
\(\begin{array}{|ll} \color{blue}u(x)=x^2-3x+6&\color{red}v(x)=x-1\\\color{blue}u'(x)=2x-1&\color{red}v'(x)=1\end{array}\)
donc \(\begin{array}{|rl}f'(x)&=\dfrac{{\color{blue}u'}{\color{red}v}-{\color{blue}u}{\color{red}v'}}{{\color{red}v}^2}\\[0,3cm]&=\dfrac{{\color{blue}(2x-3)}{\color{red}(x-1)}-{\color{blue}(x^2-3x+6)}\times{\color{red}1}}{{\color{red}(x-1)}^2}\\[0,3cm]&=\dfrac{2x^2-2x-3x+3-x^2+3x-6}{(x-1)^2}\\[0,3cm]&\color{red}\underline{=\dfrac{x^2-2x-3}{(x-1)^2}}\end{array}\)
La tangente a pour équation \(y=f'(0)(x-0)+f(0)\) avec
\(f'(0)=\dfrac{0^2-2\times0-3}{(0-1)^2}=\dfrac{-3}{1}=\underline{-3}\)
\(f(0)=-6\)
Donc \(y=-3(x-0)-6 \iff\color{red}\underline{y=-3x-6}\).
Question
4) Étudier la position de la courbe \(\mathscr C\) par rapport à la tangente \(T\).
Solution
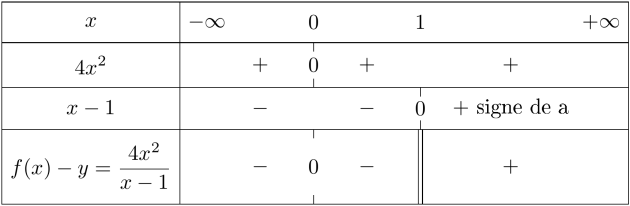
On étudie le signe de \(\begin{array}{|rl}f(x)-y&=\dfrac{x^2-3x+6}{x-1} {\color{magenta}-}({\color{magenta}-}3x{\color{magenta}-}6)\\[0,3cm]&= \dfrac{x^2-3x+6+(3x+6){\color{blue}(x-1)}}{{\color{blue}(x-1)}}\\[0,3cm]&=\dfrac{x^2-3x+6+3x^2-3x+6x-6}{x-1}\\[0,3cm]&=\dfrac{4x^2}{x-1}\end{array}\)
C'est un quotient donc on utilise un tableau de signes :
le numérateur \(4x^2=(2x)^2 \color{red}\geqslant 0\) car c'est un carré.
le dénominateur est une fonction affine avec \(x-1=0 \Leftrightarrow \color{red}x=1\) et \(a=1\) (\(\color{red}a>0\)).
On a donc :
Sur \(\color{red}]-\infty ;1[\) : \(f(x)-y\leqslant 0\iff f(x)\leqslant y\) la courbe est en dessous de la tangente.
Remarque : en \(x=0\), \(f(x)-y=0\) car la courbe touche sa tangente.
Sur \(\color{red}]1 ;+ \infty[\) : \(f(x)-y\geqslant 0 \iff f(x)\geqslant y\) la courbe est au dessus de la tangente.