Dérivation - Ex13
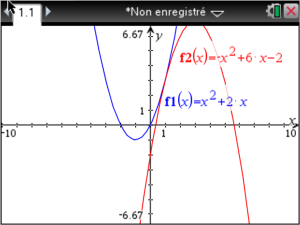
Tracer les courbes \(\mathscr C_1\, \colon \,y=x^2+2x\) et \(\mathscr C_2\, \colon\, y=-x^2+6x-2\) sur une calculatrice.
Question
1) Montrer qu'elles n'ont qu'un seul point commun \(A\) dont on déterminera les coordonnées.
Solution
\(\color{RedOrange}\text{Soient}\) \(f\) et \(g\) définie sur \(\mathbb R\) par \(f(x)=x^2+2x\) et \(g(x)=-x^2+6x-2\).
Il faut montrer qu'il n'existe qu'une valeur de \(x\) telle que \(f(x)=g(x)\).
On résout \(\begin{array}{|rcl}f(x)=g(x) &\color{RedOrange}\Leftrightarrow &x^2+2x=-x^2+6x-2\\&\color{RedOrange}\Leftrightarrow &2x^2-4x+2=0\\&\color{RedOrange}\Leftrightarrow &x^2-2x+1=0\\&\color{RedOrange}\Leftrightarrow &(x-1)^2=0\\&\color{RedOrange}\Leftrightarrow &\color{red}\underline{x=1}\end{array}\)
Les deux courbes \(\mathscr C_1=\mathscr C_f\) et \(\mathscr C_2=\mathscr C_g\) n'ont donc qu'un point commun \({\color{red}A}\left(1 ;f(1)\right)\,\color{red}\underline{=(1 ;3)}\).
Question
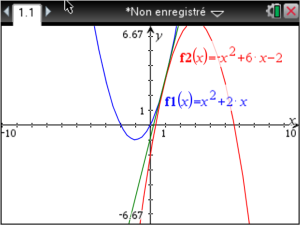
2) Montrer que \(\mathscr C_1\) et \(\mathscr C_2\) ont la même tangente en \(A\).
Note : On dit alors que \(\mathscr C_1\) et \(\mathscr C_2\) sont tangentes en \(A\).
Solution
On détermine les tangentes :
à \(\mathscr C_1\) : \(y=f'(1)(x-1)+f(1)\) avec
\(f(1)=3\)
\(f'(x)=2x+2\) donc \(f'(1)=4\).
Donc \(y=4(x-1)+3\iff\color{red}\underline{y=4x-1}\)
à \(\mathscr C_2\) : \(y=g'(1)(x-1)+g(1)\) avec
\(g(1)=3\)
\(g'(x)=-2x+6\) donc \(g'(1)=4\).
Donc \(y=4(x-1)+3\iff\color{red}\underline{y=4x-1}\)
Les deux courbes ont donc la même tangente en \(A\) et sont donc elles-mêmes tangentes entre elles.