Probabilités conditionnelles - Ex6
Question
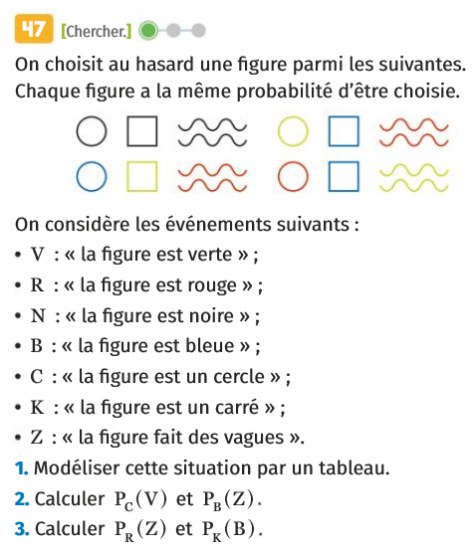
Solution
Question 1
\(V\) | \(R\) | \(N\) | \(B\) | Total | |
|---|---|---|---|---|---|
\(C\) | \(\frac{1}{12}\) | \(\frac{1}{12}\) | \(\frac{1}{12}\) | \(\frac{1}{12}\) | \(\frac{1}{3}\) |
\(K\) | \(\frac{1}{12}\) | \(0\) | \(\frac{1}{12}\) | \(\frac{1}{6}\) | \(\frac{1}{3}\) |
\(Z\) | \(\frac{1}{12}\) | \(\frac{1}{6}\) | \(\frac{1}{12}\) | \(0\) | \(\frac{1}{3}\) |
Total | \(\frac{1}{4}\) | \(\frac{1}{4}\) | \(\frac{1}{4}\) | \(\frac{1}{4}\) | \(1\) |
Question 2
\(\mathrm P_C(V)=\dfrac{\mathrm P\left(C\cap V\right)}{\mathrm P(C)}=\dfrac{\,\frac{1}{12}\,}{\frac13}\,\boxed{\color{red}=\frac{1}{4}}\)
\(\mathrm P_B(Z)=\dfrac{\mathrm P\left(B\cap Z\right)}{\mathrm P(B)}=\dfrac{\,0\,}{\frac14}\,\boxed{\color{red}=0}\)
Question 3
\(\mathrm P_R(Z)=\dfrac{\mathrm P\left(R\cap Z\right)}{\mathrm P(R)}=\dfrac{\,\frac{1}{6}\,}{\frac14}\,\boxed{\color{red}=\frac{2}{3}}\)
\(\mathrm P_K(B)=\dfrac{\mathrm P\left(B\cap K\right)}{\mathrm P(K)}=\dfrac{\,\frac16\,}{\frac13}\,\boxed{\color{red}=\frac12}\)