Savoir Faire

Méthode

Dans un repère orthonormé (O,I,J) on donne les points de coordonnées suivants :

  • R(1 ;-1)

  • S(-2 ;0)

  • T(0 ;6)

  • U(3 ;5)

  1. Vérifier la nature du repère (O,I,J).

  2. Placer les points dans le repère (O,I,J)

  3. Conjecturer la nature du quadrilatère RSTU.

  4. Calculer les longueurs RT et SU.

  5. Sachant que [RT] et [SU] se coupent en leur milieu, conclure sur la nature de RSTU.

Correction

Question 1

(O,I,J) est un repère orthonormé donc le calcul de distance avec la formule du cours est possible.

Question 2

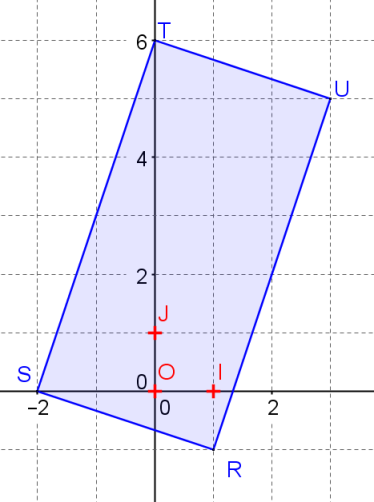
Question 3

RSTU semble être un rectangle.

AttentionQuestion 4

\(\begin{array}{rl} RT &=\sqrt{(x_T-x_R)^2+(y_T-y_R)^2} \\&=\sqrt{(0-1)^2+(6-(-1))^2}\\&=\color{red}\underline{\sqrt{50}}\end{array}\)

\(\begin{array}{rl} SU &=\sqrt{(x_U-x_S)^2+(y_U-y_S)^2} \\&=\sqrt{(3-(-2))^2+(5-0)^2}\\&=\color{red}\underline{\sqrt{50}}\end{array}\)

Question 5

RSTU a ses diagonales de longueurs égales et qui se coupent en leur milieu, donc RSTU est un rectangle.